Solution au problème : L. LAMPORT (1974)

On peut définir trois types de variables. Les variables sûres, régulières, atomiques. Pour les trois, une lecture ou une écriture seule ne pose pas de problème et fonctionne correctement.

SURE	lecture/écriture simultanée	résultat : n’importe quelle valeur que peut contenir la variable
REGULIERE		résultat : valeur avant ou après
ATOMIQUE		résultat : sérialisable

Exemple d’exécution :

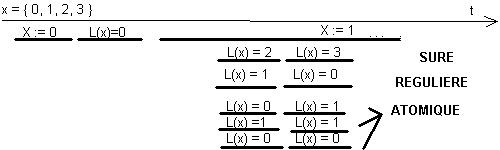
Avec des variables sûres, on a une solution qui est un mélange des solutions précédentes.
tour[i] =0 privée, représente le numéro d’ordre.
(tour[i],i) est l’identité de la requête Pi.
définition : (tour[i],i) < (tour[j],j) = ((tour[i] < tour[j]) ou (tour[i] < tour[j] et i < j))
choisir[i] = 0 privée.

Entrant choisir[i] := 1 ; tour[i] := max(tour[j])+1 ;  choisir[i] :=0 ; Dedans pour j<>i, j appartient à 1..n { tant que choisir[j]<>0 attendre ; tant que (tour[j]<>0 et (tour[i],i)> (tour[j],j) attendre ; } Section Critique ; tour[i] := 0 ;

Il est important de noter que, comme choisir bascule toujours entre 0 et 1, la variable SURE est assimilée à une variable ATOMIQUE. Lors d’une lecture/écriture de choisir[i], on peut sérialiser. En cas de crash d’un processus, il suffit de mettre ses variables à 0 pour que les autres puissent continuer.

Preuve de l’algorithme :
A1 : si pi et pj sont dedans et pi est entré dedans avant que pj ne soit entré dans Entrant alors, tour[i]A2 : si pi dans Section Critique et pk Dedans alors, (tour[i],i)<(tour[k],k)
Sureté : pi, pj (i<>j) sont en Section Critique alors A2 :
(tour[i],i)< (tour[j],j) car pi dans Section Critique et pj dedans.
(tour[j],j)< (tour[i],i) car pj dans Section Critique et pi dedans.
On a une contradiction donc on ne peut avoir deux processus en Section Critique.
Vivacité : pas d’interblocage, pas de famine (A1, FIFO).