Concept d’atomicité
|
B := A[I] |
équivaut à |
Load R1, I
Load R2 A,R1
Store R2, B |
Une instruction load est atomique, elle est exécutée en une seule fois par la machine. On appelle état la valeur des variables à un moment donné (A, B, Compteur Ordinal, …).
La sémantique d’une instruction est la suivante :
{ prédicat pré-assertion } Instruction { prédicat post-assertion }
Exemple :
{ x = a , y = b } x := y + x { x = a + b , y = b }
{ n >= 0 } x := fact(n) { x = n * n-1 * n-2 * … * 2 * 1 }
On dit qu’une opération est atomique si et seulement si elle a l’invisibilité (c’est à dire, si les états intermédiaires sont invisibles pour un observateur donné. Il ne connaît donc pas l’implémentation) et la sérialisabilité (si deux opérations atomiques sont exécutées simultanément, l’effet est le même que si elles sont exécutées séquentiellement, quel que soit l’ordre choisit). On a une abstraction par rapport, d’une part à l’espace (qui concerne la mémoire) et d’autre part au temps. Le principe de sérialisabilité permet d’assimiler une instruction à une opération instantanée.
Exemple :
|
Y := 0 (a)
X := 0 (b) |
|
X := y + z (c) |
Y := 1 (d)
Z := 2 (e) |
|
… |
Au cours du temps, on 4 cas différents peuvent se produire :
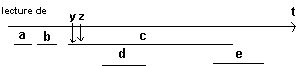 |
on obtient x=0, y=1 et z=2, ce cas équivaut à effet(cde). |
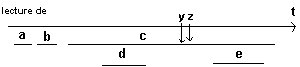 |
on obtient x=1, y=1 et z=2, ce cas équivaut à effet(dce). |
 |
on obtient x=2, y=1 et z=2, ce cas équivaut à effet(c1 d e c2). Si l’effet(c // de) donne x=2 alors, l’opération n’est pas atomique. On évitera ce type d’opération (on a un cycle, on ne peut pas transformer en séquence). |
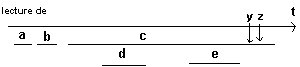 |
on obtient x=3, y=1 et z=2, ce cas équivaut à effet(dec). |
Donc, si effet(c // de) = effet (cde) ou effet(dec) ou effet(dce) alors on a une opération atomique.
La problématique est de savoir construire des opérations atomiques et de synchroniser et faire coopérer ces opérations. |

